物質は膨大な多様性を持っていますが、その極一部しか知られていないのが現状です。それを補うための強力なツールとして数値シミュレーションが注目されています。計算機の能力が年々指数関数的に伸びるにつれて、新たな研究が可能になっています。主なテーマをいくつか紹介します。
テーマ①多体摂動論を用いた電子状態計算
計算物質科学の最前線は励起状態にまで拡大しています。多粒子グリーン関数法を用いた計算により励起エネルギーや励起子の波動関数$latex \Psi\left( \vec{r}_{e},\vec{r}_{h}\right)$などの電子状態の情報が得られるようになったためです。物質内での電子($latex \vec{r}_{e}$)と正孔($latex \vec{r}_{h}$)の分布がわかると、励起後のダイナミクスを調べることが可能になります。
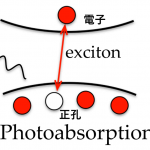
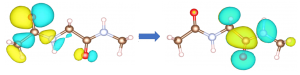
励起(左図)。右図は励起子波動関数の主成分(左は正孔、右は電子)
杉野研究室では最近、下図のような新たに合成されたナノカーボン分子(~200原子系)の計算を行い、この物質の光学特性を明らかにしました。この他、発光素子や太陽電池の材料となる物質の研究も行いました。
最近計算を行ったナノカーボン分子
これまでは励起ダイナミクスを研究するのに、実験データの解析から導出された模型が主に用いられてきました。しかしながら模型を精巧化して定量的な理論予測をすることは困難です。実験からの情報には限りがあるからです。仮に原子配置などの微視的な情報が得られたとしても、そこから直接模型の精巧化につなげることはできません。励起状態の計算が必要なゆえんがここにあります。詳しくは(2)で説明します。
テーマ②密度汎関数理論を用いた電極界面の計算
電極と水溶液の界面(電極問題)は計算物質科学の重要なテーマです。杉野研究室では密度汎関数理論とよばれる多電子系の計算手法に基づき、電位差がかかっている固体と液体の界面のシミュレーションを行っています(下図)。燃料電池反応がなぜ白金で高効率で起こるのか、どのようなメカニズムで起こるのか、白金を超える電極物質はどのようなものがあるのかなど、長年の謎の解決につながる研究を行っています。
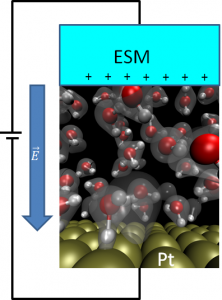
ESMとよばれる有効媒質を用いた白金と水溶液界面の計算模型
計算には、一般的な密度汎関数理論だけでなく乱雑位相近似レベルの高精度理論も用いる必要があります。計算ではまた、溶液側および固体側での(静電)遮蔽の取り扱いも重要となります。計算手法の開拓が重要な研究テーマです。
テーマ③ホタルの生物発光
生体物質と水の界面も重要なターゲットです。生物発光はノーベル賞を受賞された下村先生の御研究テーマでもありますが、なぜ生体内では非常に効率的な発光が可能なのかなど謎が残っています。ホタルの発光に関してはオキシルシフェリンという分子が担っていますが、その基礎物性に関してすらあまりわかっていません。そこで杉野研究室では物性研の秋山研究室と共同で密度汎関数理論を用いた長時間シミュレーションを行いました。その結果、オキシルシフェリンの安定性には水との界面の詳細が大きく関与していることを突き止めました。従来は水の誘電的性質のみが安定性に効いているという考えが支配的でしたが、実はもっと複雑な要因で安定性が決まっていることがわかりました。
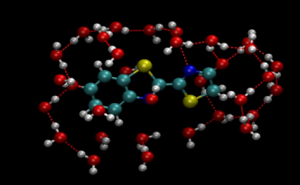
オキシルシフェリン分子と取り囲む水分子
テーマ④ 負の誘電率
二種類の固体が作る界面も興味深いテーマです。強誘電体の誘電率は正の値となりますが、電場をかけて分極が変化している途中では誘電率は負の値を取ります(ランダウ理論)。その途中の状態は不安定ですので負の誘電率が測定されることはありません。しかし界面では準安定になることがあります。実際には界面を安定化させようとする様々な要因がありますので、それに打ち勝って準安定状態が実現し得るかどうかを調べる必要があります。そこで東大のマテリアル工学科の渡邉研究室と共同で、密度汎関数理論計算を用いた研究を行いました。強誘電体と常誘電体が作る薄膜で誘電率を調べてみると、果たして準安定状態が実現することがわかってきました。負の誘電率が実現されれば半導体デバイスの微小化が可能になりますので、そのための基礎研究が進んだと言えます。
テーマ⑤固体酸素
固体酸素は低温あるいは高圧の下で存在していますが、ファンデルワールス力と磁気相互作用が競合することにより様々な物質相が現れます。通常の密度汎関数理論に対して磁気相互作用を経験的な方法で補正を施すことにより、定量的に計算ができることがわかりました。固体酸素に強い磁場をかけると磁気モーメントが揃うような構造に相転移相転移することが知られていますが、必要な磁場の強さに関する予測計算を行いました。
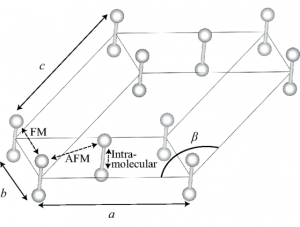
固体酸素(α相)の構造
テーマ⑥ヒドロキシアパタイト
ヒドロキシアパタイトは人骨の主成分ですが、イオン伝導性と様々な誘電性を併せ持つ興味深い物質としても知られています。イオン伝導性と誘電性がどのように関連しているのかを密度汎関数理論に基づく動力学計算などから明らかにしました。
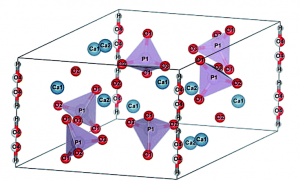
ヒドロキシアパタイトCa10(PO4)6(OH)2の構造
その他
その他実験との共同研究から新たなトポロジカル絶縁体物質などに関する成果が得られています。








