Our condensed matter research is based on numerical simulation. This group consists of 11 members; one professor, one research associate, two ISSP research fellow, two postdocs, four students, and one office administrator.
Main targets are (1) material research using the numerical simulation and (2) development of the simulation scheme.
(1)Material Simulation
Diversity in materials is indeed diverse. We know only very small piece of the whole picture. As a powerful means to supplement the picture, material simulations are attracting attention. The role of the simulation is extending year by year. This is because computers are rapidly enhancing the power and the methods of simulation are made sophisticated.
(a) Electronic structure from the many-body perturbation theory (GW + Bethe-Salpeter equation method)
One of the most important frontiers is in the excited state study. The study is boosted by the development of many-body Green’s function methods to obtain the excitation energy and the wave function of the excited electrons and holes. With these quantities, it is possible to study the dynamics initiated by an electron excitation.
The excited state dynamics has traditionally been studied by using a model empirically determined from experimental data, but the model cannot be improved when the experimental data is scarce. Detailed structural data alone may not be necessarily sufficient; information of electronic structures may be additionally required.
The electron and hole does not independently propagate, but these quasiparticles are interacting in the excited states. The propagation can be described by the many-body Green’s function method. The equation of motion for Green’s function has a form similar to the Bethe-Salpeter equation (BSE) frequently used in high-energy physics, so that the same name is used in condensed matter. BSE is solved after reformulated into an eigenvalue problem. BSE is most frequently formulated using approximations like GW approximation, so that the method is called GW + BSE.
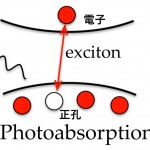
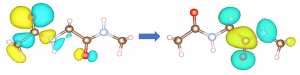
Electronic excited state initiated by photoabsorotion (leftmost), and the wave function for the hole (middle) and electron (rightmost).
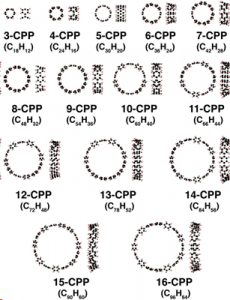
Nanocarbon molecules
We study the excited states using the GW + BSE simulation together with experimental data available. This simulation is very demanding; the computational time scales as the sixth power of the number of atoms for solids, O(N6), while the scaling is weaker for isolated molecules, O(N3-4). When utilizing the massively parallel computers, it is possible to calculate a system containing up to two hundred atoms within a week. We have used our in-house code to study nanocarbon molecules (see figure). We have predicted optical spectrum of materials which may work as a luminescence or photovoltaic material.
(b) Electrode-solution interface
We have applied our method, effective screening medium (ESM), to solid-liquid interfaces to understand the electrochemical phenomena, such as the fuel-cell reaction or water splitting. ESM allows us to apply bias potential to the interface (see figure) and investigate the atomic scale details on the “electrode dynamics”. We are studying the platinum-solution interface as well as the oxide-solution interfaces as a possible platinum substituting cathode material.
We have recently found that the theoretical prediction actually depends sensitively on the accuracy of the electronic structure calculation. In this context, we use the random phase approximation (RPA) within the density functional theory (DFT) to correct some of the results obtained using the standard DFT.
For semiconducting electrodes, screening of the surface charge occurs both the solution side and the solid side. In other words, the electric double layers induced on both sides compete and give rise to rich variety of the interface phenomena. With our new methods, we are studying such varieties.
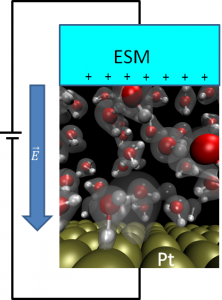
Our model for the electrode-solution interface.
(c) Firefly oxyluciferin
Biomaterials are functional when interfaced with solution. So, the interface is a key to understanding the biofunction. Among many biomaterials, we are currently targeting oxyluciferin molecule which plays a role as the luminescence center of fireflies. There are controversies about the stability of oxyluciferins in solution presumably due to lack of microscopic understanding of the interface. With this in mind we have performed a very time-consuming simulation to find that the previous understanding is too approximate. The water molecules are interfaced complicatedly with oxyluciferin according to the complicated charge distribution within the molecule. Contrary to the previous picture, behavior of water molecules is thus directly concerned with the stability in solution. The next step of this project is then to understand the mechanism of the luminescence.
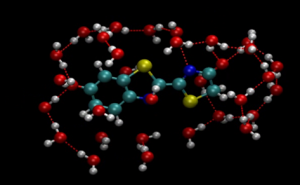
Oxyluciferin molecule surrounded by water molecules
(d) Negative capacitance
Solid can be made functional when interfaced with other solid. Ferroelectric materials have a positive capacitance, but this is not the case when the material is transiently changing the polarization. The negative capacitance thereby appearing is unstable and cannot be measured in the bulk as the Landau theory explains, but can be made metastable at an interface. The possibility is investigated at a ferroelectric thin film interfaced with a paraelectric thin film to find that the structure of the negative capacitance can indeed survive against the driving force to form a domain structure, which make the capacitance positive. Negative capacitance has been attracting attention as a means to enhancing the total capacitance of an electronic device.
(e) Solid oxygen
Solid oxygen exists under a low temperature or high pressure condition. The structure is determined by delicate balance between the van der Waals interaction and magnetic interaction. When the density functional theory is empirically modified using the effective on-site Coulomb, the balance can be reasonably well simulated. We have found that the low-temperature phase (see figure) can be predicted by theory. The theory is used then to predict an unknown high magnetic phase, in consistent with experiment.
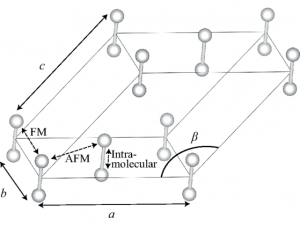
Structure of the α-phase of solid oxygen
(e) Hydroxyapatite
Hydroxyapatite is a material comprising up to 50% of bone. This material is also known to exhibit ionic conductivity and piero-, pyro-, and ferro-electricity. We have performed the first-principles calculation to investigate the mechanism for the polarization. We have found several processes are concerned including flipping of OH-, exchange of proton vacancy, and the hopping of the OH- vacancy, in consistent with the experiments.
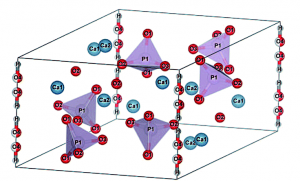
Structure of the hydroxyapatite (Ca10(PO4)6(OH)2).
Other topics
We are also investigating materials in collaboration with experimental researchers, such as phase transition of MnP and new topological insulators.
(2)Development of computational method
To advance the computational materials science, one need to develop novel computational method and intentionally extend the frontier of the simulation; the frontier is always changing when computers speedup. We need to extend the method for (a) solving the many-body Schrodinger equation to obtain the electronic ground and excited states, (b) obtaining the most stable structures, (c) calculating the response to external perturbations, (d) obtaining the thermodynamic states, and so on. Many works have been done also to develop multi-physics methods to bridge macroscopic phenomena with the micros, which is nontrivial for inhomogeneous materials with or without chemical reactions, such as biomaterials.
Density functional theory (DFT) has been accepted as the standard method for the computational materials science. This theory is based on the Hohenber-Kohn theorem which establishes one-to-one correspondence between (a) the ground state and (b) the particle density together with the functionals to relate (a) and (b) developed by many researchers in the past half century. The theory has not been successfully developed for strongly correlated systems and some of the excited states. Because of this, other computational methods other than DFT are also paid attention.
Success of DFT does not immediately mean that we can apply DFT to large systems because of the large gap existing between micro and macro. DFT provides the ground state of a given atomic geometry, but interesting phenomena often occur in systems where many metastable states with equal energy exist. Then it is not trivial to find the most stable, or a thermodynamically stable, structure.
Many body wave function theory — tensor decomposition method —
N electron systems in a material can be characterized by the many-body wave function with 3N degrees of freedom. Determining the wave function in the vast Hilbert space is an ultimate goal.
The wave function is specified by the anti-symmetric tensor of degree N. If the degrees of freedom can be encoded very compactly, there may be a way to handle the wave function. As a way of the encoding, there is a technique called tensor decomposition, with which to decompose the original tensor into a product of tensors of lower degrees. This group is developing an algorithm for this purpose.
Many-body perturbation method
The electronic structure can be described by the Green’s function for the many-body Schrodinger equation. The Green’s function can be used to describe not only the ground state but also the excited states, which are generated by shining a light. The Green’s function is obtained by solving the Bethe-Salpeter equation for the excited electrons and holes. In practice the equation is reformulated into an eigen problem using some approximations to the Feynman diagrams such as the one called GW. This group develops algorithms for the GW + BSE calculation and also an inhouse code.
Interface
When a material is interfaced with another material of large permittivity, such as ferroelectric materials and liquid water, charged particles can be stabilized at the interface because of the dielectrically reduced Coulomb energy. The interface thus provides a field for the exchange of charge (and also exchange of energy), which is applied to various batteries and bio-membranes. When the Coulombic field extends deep inside the materials, the microscopic details occurring at the interface are coupled to the bulk, yielding thereby many interesting phenomena. This is one of the targets of interface science.
In a practical DFT simulation, it is not trivial to describe the long-range Coulombic field. The interfaces thus require methodological development to initiate the study. Actually, many researchers are enjoying the development. Our group is developing a methodology for (a) platinum-solution interface with which to construct a microscopic theory for fuel cells and for (b) the solid-solid interface to deepen understanding on, for example, the space charge layer.
Education
Sugino group participates in the physics department of the graduate school of the University of Tokyo. http://www.issp.u-tokyo.ac.jp/maincontents/education_en.html
Please visit Department of Physics for details.

