Effective Screening Medium（ESM）
Effective Screening Medium（ESM）
This is an official place to find the novel computational scheme of "effective screening medium" (ESM) method developed originally by M. Otani and O. Sugino Phys. Rev. B 73, 115407 (2006)
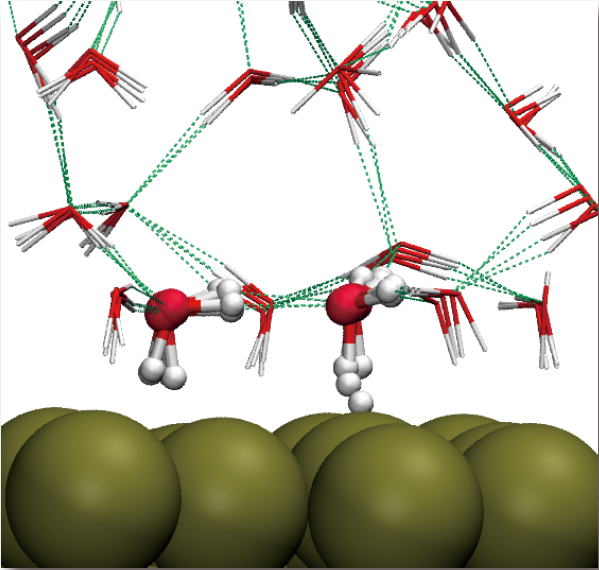
The ESM scheme has proven effective in simulating the metal/water interface, but also made simpler the charged-up surfaces in general.
ESM?: What can be done?
This method enable to describe the surface and interface, e.g. a slab system that is periodic in the direction parallel to the surface but is arbitrary shape in the perpendicular direction, sandwiched by semi-infinite media, such as vacuum, an electrode, or an electrolyte. Here, we call the medium "effective screening medium" (ESM).
The ESM model enables to model the polarized surface without dipole correction.
News
- SIESTA+ESM version 1.05 (!!IMPORTANT!! includes bug fix for bc2 condition, Support for Siesta-3.1, 2012/06/14) available
Introduction
What is Effective Screening Medium (ESM) method?
Effective Screening Medium (ESM) method uses for the surface the slab model periodic in surface parallel directions, as is commonly done in the first-principles calculations, and describes the screening effect by introducing local relative permittivity 
and classical charge 
into the slab model.
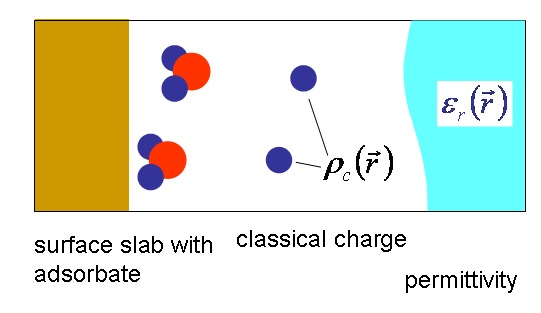
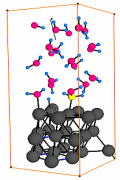
For example, in order to model the STM tip, we introduce region of infinite relative permittivity, e.g., the blue region in the above figure, which we will call as ESM region. To model the solution, on the other hand, we introduce ESM region with 
to mimic the screening effect of the water and classical charges to mimic the electrolyte ions. (It is considered better to add quantum water near the surface as shown in the figure.)
Importantly, the effect of can be incorporated as a boundary condition for the Poisson equation and we do not have to explicitly treat the whole region. This allows us to use infinitely thick region for the ESM, i.e., isolated slab model, which is particularly important to describe the system with long-range Coulomb interaction. Note that, in our quasi one-dimensional model, the line of electric force extends infinitely if screening effect does not exist.
We may use effective point charges for , but we can also conveniently use continuum model for the classical charge distribution, such as the Poisson-Boltzmann model to relate to the electrostatic potential 
according to the Maxwell-Boltzmann distribution.
Since we are using isolated slab model, we can use the potential at infinity 
as the reference. This allows us to unambiguously introduce the bias voltage as is done experimentally
Continue to Basic formulation of ESM.
Research Activities
Here, we describe some of our research activities based on the ESM scheme.
Charged Surfaces --- a First-Principles Approach
The ESM scheme has proven effective in simulating the metal/water interface, but also made simpler the charged-up surfaces in general.
Simulation on the Electrode Dynamics
Support and Help
General questions
- Minoru OTANI :
- Osamu SUGINO :
OpenMX+ESM
- Tsukuru Ohwaki :
SIESTA+ESM
- Yoshinari TAKIMOTO :
STATE+ESM
- Ikutaro HAMADA :
TAPP+ESM
- Kazuto AKAGI :
