Documentation
Continued from the top page introduction.
Basic formulation of ESM
The total energy expression for the ESM method is given as
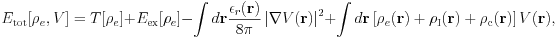
which is different from that for the conventional slab in that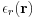 
and 
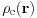are introduced. Here we use an expression where the electrostatic potential is taken as the variational parameter for our convenience. The above equation can be rewritten as
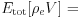
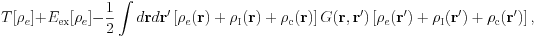
when the Green's function for the Poisson equation
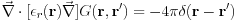
is introduced. The Kohn-Sham equation, derived by varying the total energy with the Kohn-Sham orbital, is not affected by the ESM, but the Poisson equation, derived from electrostatic potential variation, is affected as
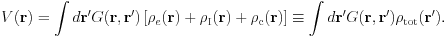
So the most time-consuming part, the Kohn-Sham equation, remains unchanged and the ESM calculation is then as feasible as the conventional first-principles calculation when much less time-consuming part, the Poisson equation, can be handled reasonably efficiently.
1. Expression for G
Here we show four examples where the Green's function can be simply written. We focus on the special case where the relative permittivity depends only on . Then the Poisson equation, in the Laue representation, is
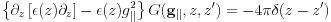
where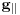 
is a reciprocal lattice vector in the surface parallel direction and 
.
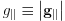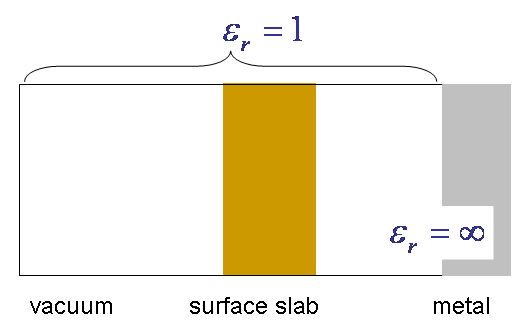
(i) vacuum/slab/vacuum
The first example is a trivial one where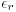 
is everywhere equal to one, which means the slab is embedded in infinite vacuum.
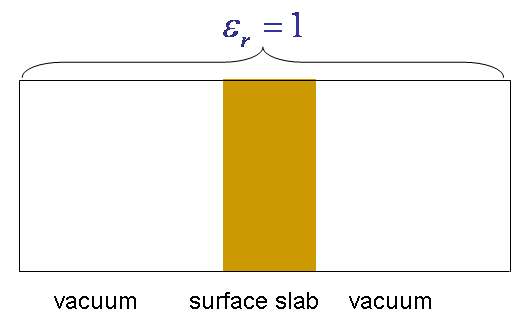
The boundary condition for the Poisson equation is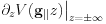 
, and the Green's function is
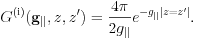
When ,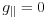 
it is
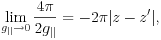
with the first diverging term giving no contribution to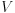 
when neutral.
Note that this Green's function corresponds to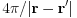 
when represented in real space. So, this will be also denoted as 
.
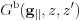(ii) metal/slab/metal
The second is the slab sandwiched by semi-infinite metals:
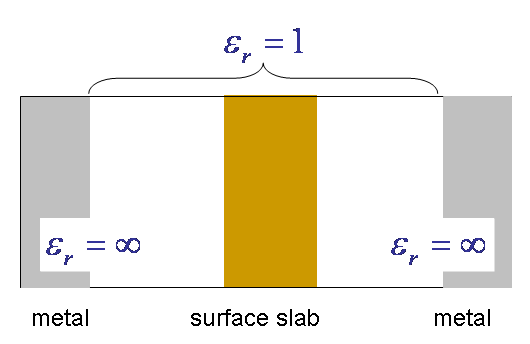
The boundary condition is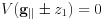 
,
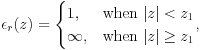
and the Green's function is
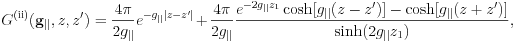
in the region where both 
and 
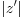are smaller than 
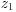. When 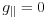, it is
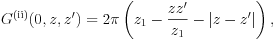
indicating a linear dependence of the Coulomb potential for one-dimensional system.
(iii) vacuum/slab/metal
The third is the slab with the metal attached on the right:
The boundary condition is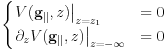 
,
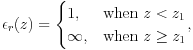
and the Green's function is
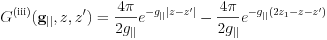
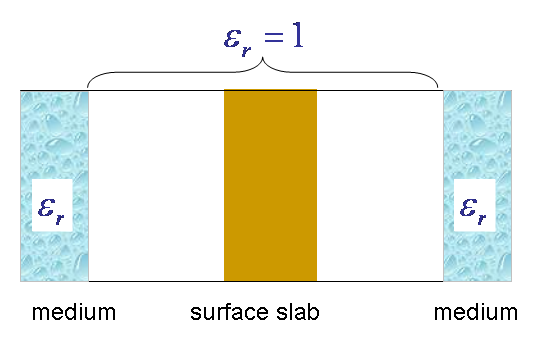
(iv) medium/slab/medium
The fourth is the slab sandwiched by semi-infinite media with finite :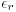
The boundary condition is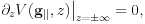 
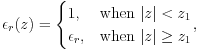
and the Green's function is
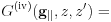
when both and are smaller than .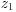
These Green's functions allow us to integrate analytically to obtain the electrostatic potential when the charge density is expanded into Fourier series. In that case the computational task to solve the Poisson equation is negligible.
Note that these Green's functions are rewritten as the bare Coulomb term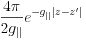 
plus series of image terms, which is
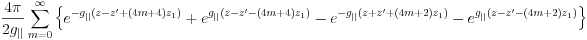
for the boundary condition (ii) and is
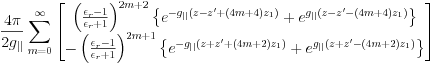
for the boundary condition (iv).
2. Ewald summation
To compute the interaction among the point charges, i.e., nuclear charges and classical charges , we use the Ewald summation technique. Since we are using isolated slab, interaction between two-dimensionally repeated replica needs to be summed up, with the typical form being
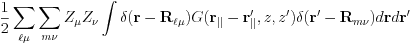
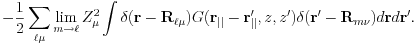
The delta-function,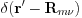 
, is partitioned into
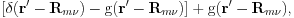
where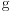 
is a Gaussian function, and the first term is integrated in real space and the second term in reciprocal space. Importantly, the image terms in the Green's function give null contribution to the real space integration, leaving only the bare Coulomb term. Note that the bare Coulomb term appears also in the conventional first-principles calculation and can be easily integrated. The reciprocal space integration is straightforward because we know explicit form for the Green's function.
3. Total energy expression for the ESM
Once the total energy is formulated, it is straightforward to derive the equation of motion for the nuclear motion. We start from defining the total grand potential by adding to the total energy the nuclear kinetic energy and by subtracting as
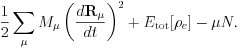
By taking a variation with respect to the nuclear coodinate, we obtain the atomic force, which is equal to the Hellmann-Feynman force.
Implementation and applications
The ESM method needs modification of the Poisson solver and the Ewald summation only, and may be easily implemented to existing first-principles program packages. So far, it has been implemented to TAPP (Tokyo Ab-initio Program Package) and STATE (Simulation Tool for Atom Technology), standard packages in Japan. Several groups are now doing intensive calculations on biased surfaces or nanostructures, such as electrochemical reactions on Pt surface, organic molecules on Si surface, and carbon nanotubes on backgate.
